Biologically-Plausible Learning Algorithms Can Scale to Large Datasets by Will Xiao[1], Honglin Chen[2], Qianli Liao[2] and Tomaso Poggio[2]
[1] Department of Molecular and Cellular Biology, Harvard University
[2] Center for Brains, Minds, and Machines, MIT
Background
Consider a layer in a feedforward neural network. Let xi denote the input to the i th neuron in the layer and yj the output of the j th neuron. Let W denote the feedforward weight matrix and Wij the connection between input xi and output y. Let f denote the activation function. Then, Equation 1 describes the computation in the feedforward step. The feedback step propagates the error signals using equation 2.
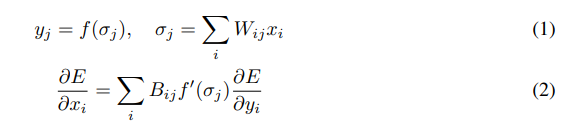
-
If B=W we have standard backpropagation algorithm
-
Sign Symmetry Backpropagation Algorithm has B = sign(W)
-
Feedback Alignment Backpropagation Algorithm has B as a random fixed matrix
Conclusions
SIGN SYMMETRY
Imagenet:
-
Sign symmetry only slightly underperformed Backprop on Imagenet.
-
No effect of having backprop in the last layer unlike FA
-
Better than FA likely because sign information allows for easier feedforward and feedback weights alignment
FEEDBACK ALIGNMENT
According to lilicrap et. al even though the feedback weights are random the error signals still lie within the 90 degrees of true error signals calculated from backprop. Thus the model is still capable of moving along the real direction.
Imagenet:
-
Better than reported by bartunov et al if backprop used to train the final classification. The authors claim the exact error calculation (loss evaluation) is likely not softmax so it can come by a different mechanism.
-
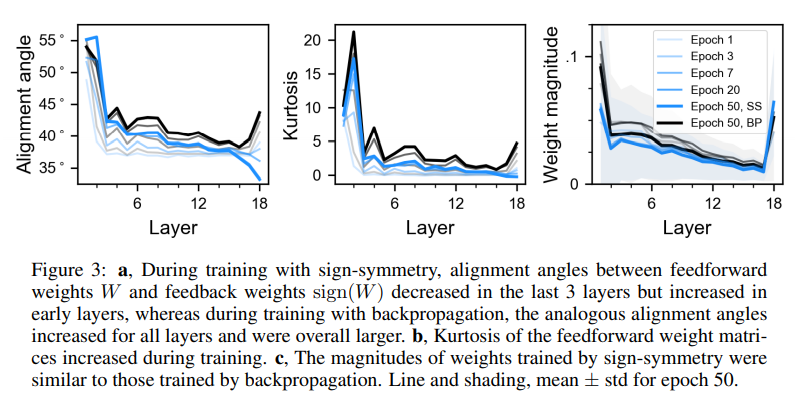
Lillicrap et al. (2016) show that with feedback alignment, the alignment angles between feedforward and feedback weights gradually decrease because the feedforward weights learn to align with the feedback weights
Interesting lines of work and validation experiments
- The existence of the feedforward and feedback pathways specifically aligned in an antiparallel way to justify sign symmetry.
- Incorporation of Dale’s Law so as to ensure neurons don’t change their sign during the entire learning process. BP, FA, all of the TP variants, and indeed most known activation propagation algorithms (for an exception see Sacramento et al), still require distinct forward and backward (or “positive” and “negative”) phases. The existence of these phases is still a matter of research.
- I would like to understand how the feedback pathway will behave on continuous error signals or long term errors. Like with our previous discussions, based on region and cell type they specifically undergo LTP or LTD.